BullsEye: Scalable and Accurate Approximation Framework for Cache Miss Calculation

Nilesh Shah, Ashitabh Misra, Antoine Miné, Rakesh Venkat, and Ramakrishna Upadrasta

Published in ACM TACO

BullsEye, a novel, scalable, accurate, and problem-size independent approximation framework. It is an analytical cache model for fully associative caches with LRU replacement policy focusing on sampling and linearization of non-affine stack distance polynomials. Firstly, we propose a simple domain sampling method that can improve the scalability of exact enumeration. Secondly, we propose linearization techniques relying on Handelman’s theorem, and Bernstein’s representation. To improve the scalability of the Handelman’s theorem linearization technique, we propose template (Interval or Octagon) sub-polyhedral approximations.

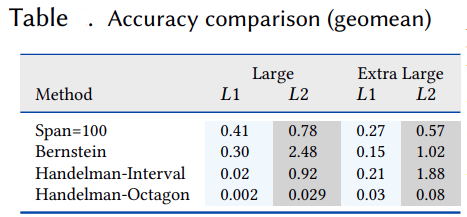
We propose various approximations of Miss set 𝑀:(i) SparseEnum: a simple statistical approximation and (ii) Two linearization methods, where the mathematical theory is based on Handelman’s theorem and Bernstein representation of polynomials. We extend the earlier characterization of positive polynomials over a polytope by Feautrier, and polynomial linearizations by Maréchal et al. For scalable solutions, we propose to approximate 𝑀 using sub-polyhedral (interval and octagon) template polyhedra to provide a highly scalable linearization. Another linearization is proposed based on mathematical theory of Bernstein polynomials, and Bernstein expansion over convex polytope by Clauss et al.

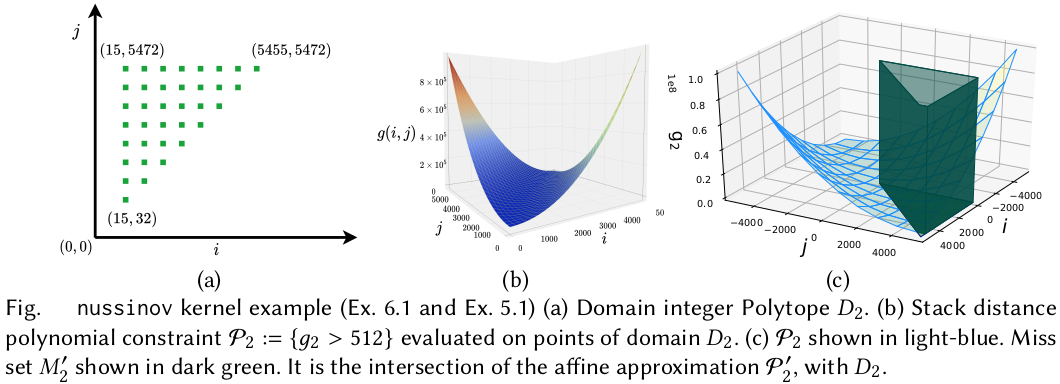
Sampling and Linearization of Stack distance polynomials

Sparse Enum

Handelman theorem based Sub-polyhedral (Interval/Octagon) Linearization

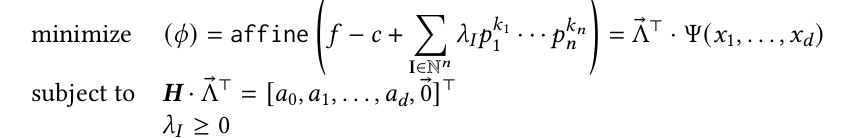The above equation describes a parametric LP formulation the cost function of which is parametric; both Λ-vector and Ψ-vector are unknown. The constraints however describe a normal (non-parametric) polyhedron in Λ. Such a formulation could be solved using a parametric rational linear solver, like the MPT solver to obtain 𝜙. We propose a novel method, that avoids calling a parametric solver, resulting in a set of non-parametric cost functions, through the following steps: (i) restricting the shape of the affine form 𝜙 to a fixed template (intervals/octagons), and (ii) instantiating the parameter vector (Ψ) using vertices (of domain 𝐷′) to obtain a non-parametric cost function.

Example:

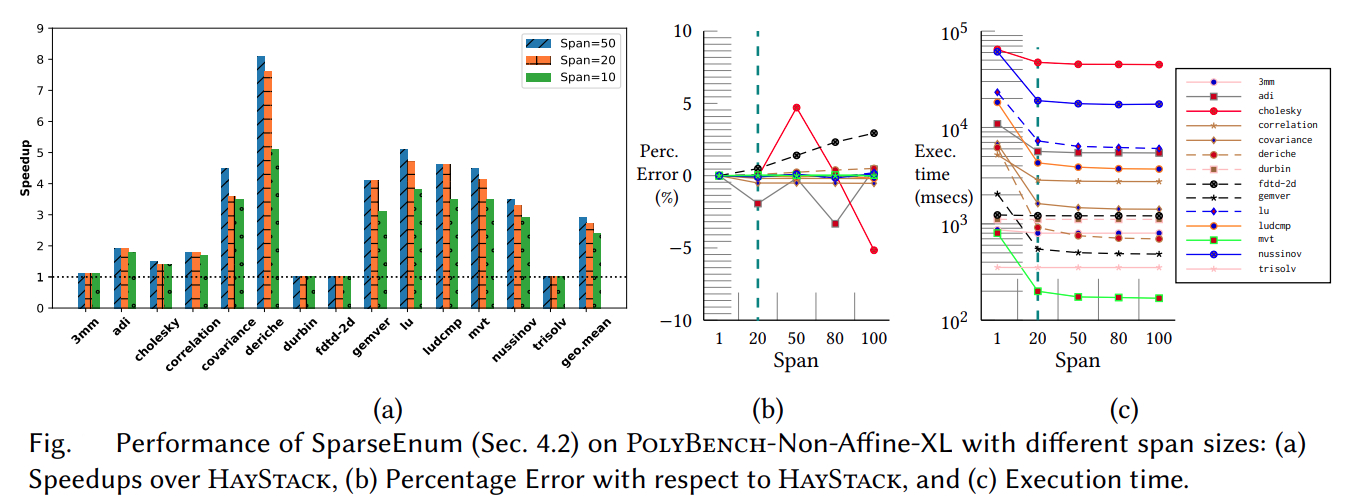
Performance and accuracy

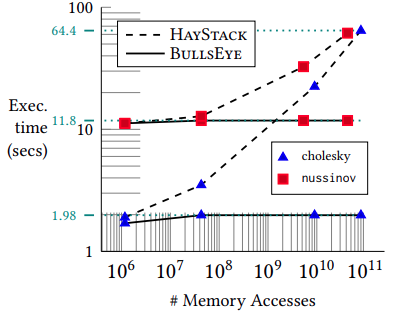
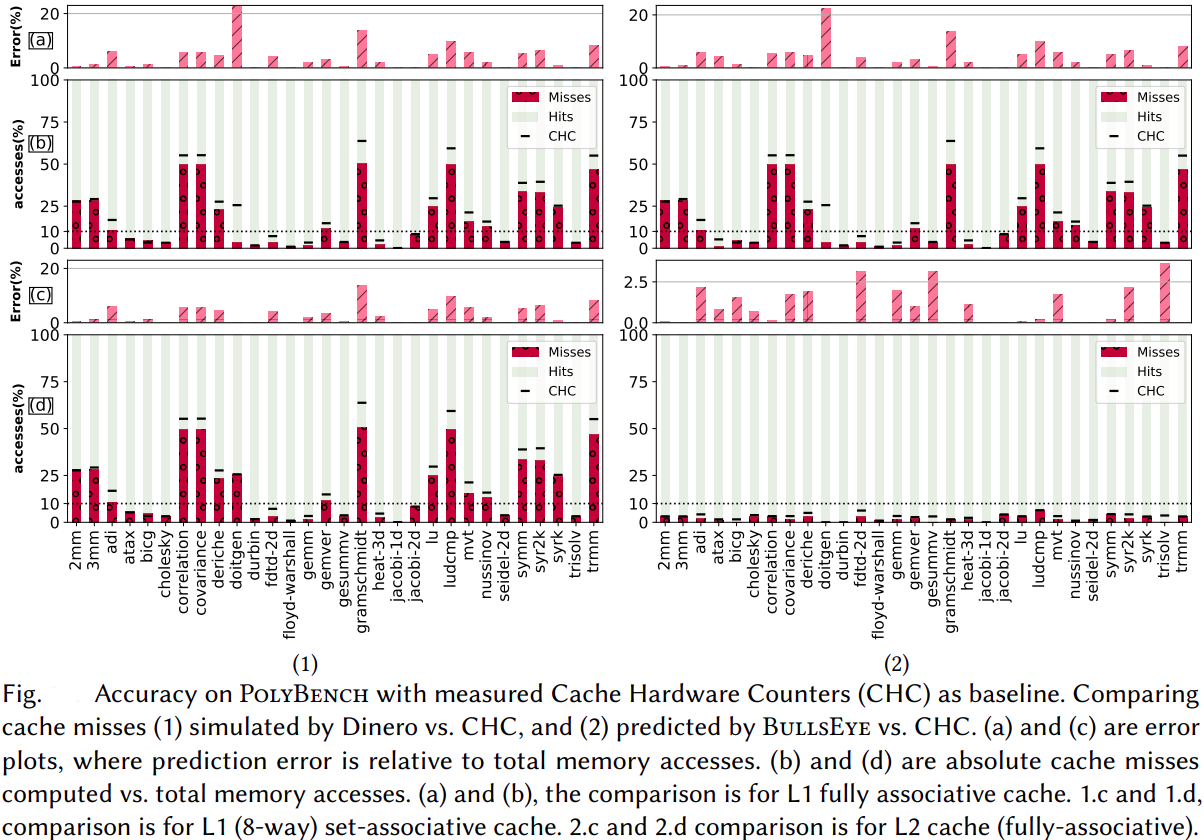
Our methods obtain significant compile-time improvements with high-accuracy when compared to HayStack on important polyhedral compilation kernels such as nussinov, cholesky, and adi from PolyBench, and harris, gaussianblur from LLVM-TestSuite. Overall, on PolyBench kernels, our methods show upto 3.31× (geomean) speedup with errors below ≈ 0.08% (geomean) for the octagon sub-polyhedral approximation. We show the execution time comparison of HayStack vs. our new approximate cache miss framework BullsEye. We obtain maximum speedups of 5.2× and 32.5×, and maximum errors of 0.82% and 0.55% for nussinov and cholesky respectively. It can be seen that our approximation provides good scalability and accuracy; it is also input problem-size independent.

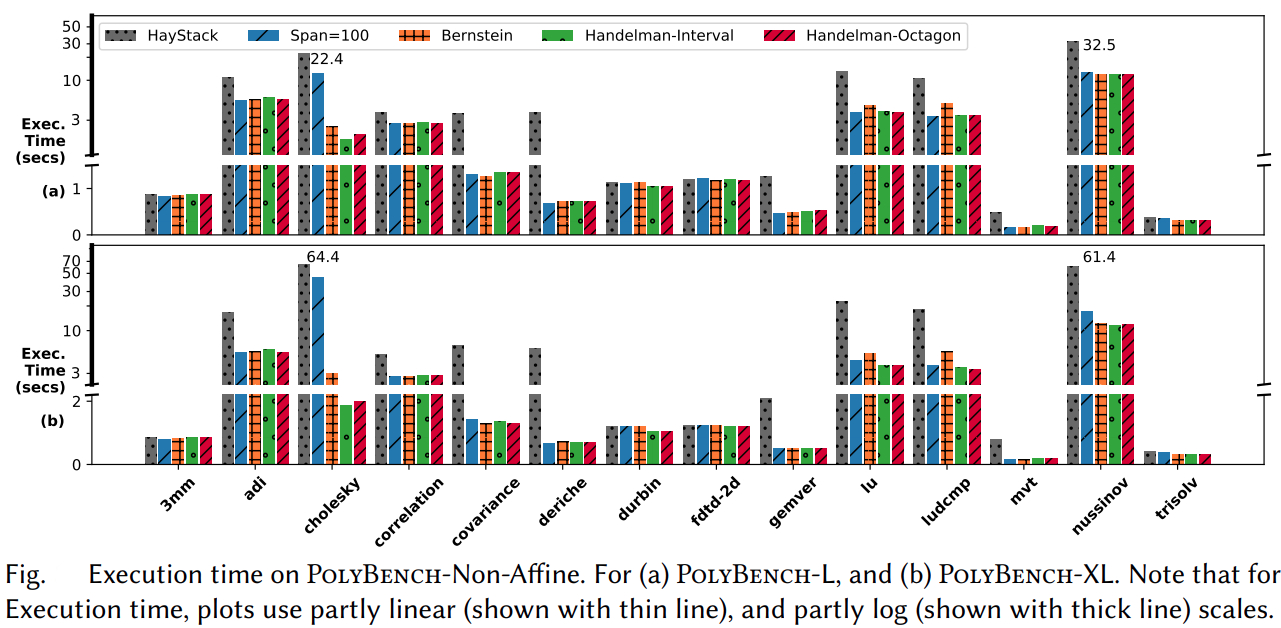
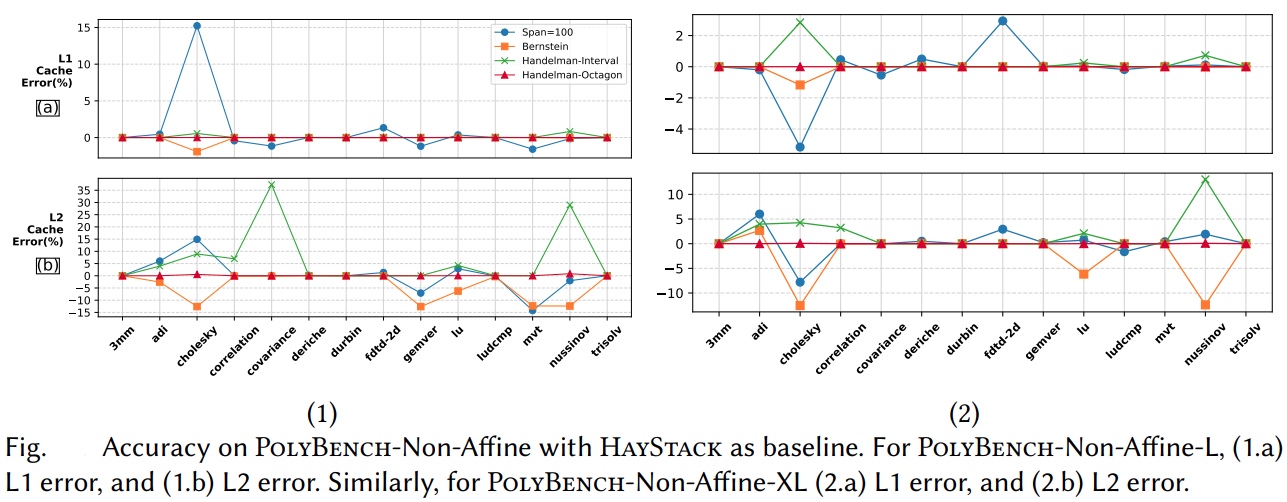
Artifacts

Code and other artifacts will be available on our GitHub page.

Funding

This research is funded by the Department of Electronics & Information Technology and the Ministry of Communications & Information Technology, Government of India. This work has been partly supported by the funding received from DST, Govt of India, through the Data Science cluster of the ICPS program (DST/ICPS/CLUSTER/Data Science/2018/General), and an NSM research grant (MeitY/R&D/HPC/2(1)/2014).